Axiomatic bargaining

The principles of axiomatic bargaining are illustrated by studying further the problem of the commons faced by Harold and William in axiomatic bargaining.

It is commonly approved that a solution should desirably satisfy Pareto optimality in any bargaining or negotiation situation. This is because it guarantees that there exists no other outcome unanimously preferred by each player. Pareto optimality alone does not, however, offer a unique solution but a set of efficient solutions that are more or less preferable from a player’s viewpoint. The paradigm of choosing a fair Pareto optimal solution for a game is addressed by axiomatic bargaining theory that is a field of game theory. It consists of formulating axioms on how a solution for a set of games should be selected and checking if the implied solutions seem appealing, see, e.g., Thomson and Lensberg (1989; especially Chapter 2).

Originally Nash (1950) introduced this axiomatic approach by presenting the Nash bargaining solution, which is an outcome maximizing the product of utilities perceived by the players, and the related axioms. Some of Nash’s axioms were criticized in the literature and consequently several modifications were presented. The best known variation of Nash bargaining solution, the Kalai-Smorodinsky solution, was contributed by Kalai and Smorodinsky (1975). As game theory, axiomatic bargaining is descriptive in its nature too and it does not either offer practical aid on how to reach the outcomes implied by the axioms in practice.

The bargaining problem

… establishing co-operation …

Harold and William ended up to the competitive Nash equilibrium and they are worried about overutilizing the green. Hence they sit in a negotiation table and work co-operatively to find a fair, jointly satisfying and Pareto optimal solution, or agreement, for their problem.

… bargaining problem in the utility set …

Axiomatic bargaining describes the bargaining problem in the utility set, which is the set of possible payoff pairs the players can receive. The players can construct the utility set by plotting the payoff pairs for each possible strategy pair in (u_H,u_W)-plane, see figure below.

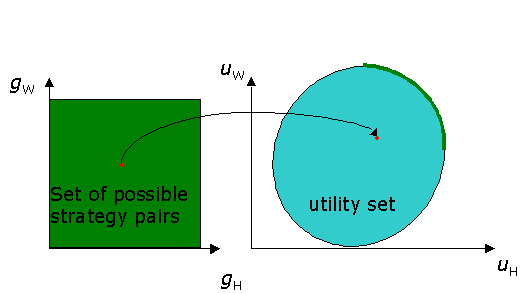
The green bolded frontier in the utility set indicates the Pareto optimal payoff pairs.

Text Box: By definition, the problem of selecting a particular point in the utility set is called the bargaining problem.

… what if their co-operation fails? …

If Harold and William can find a jointly accepted point in the utility set, then they get it. However, if they fail to agree, then they end up to the disagreement point d=(d_H,d_W). In this game, the disagreement point is the payoff pair implied by the non-cooperative solution, the Nash equilibrium strategy pair, and hence

… the role of the disagreement point? …

Harold and William plot now the disagreement point d in the utility set.

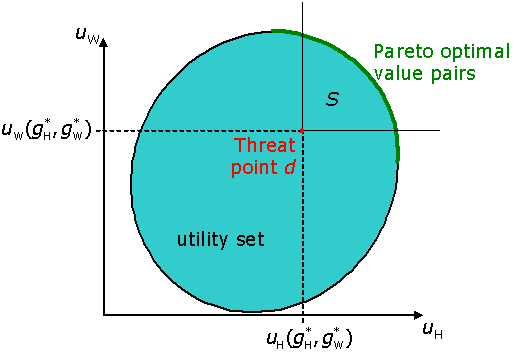
The players are not willing to choose any point in the utility set, because some of them yield worse payoff for them than the threat agreement. Therefore, they search for a solution only in the subset S that consists of the payoff pairs that are jointly preferred to d.

Obviously, the players should now select a Pareto optimal point in the utility set, but which one of them is fair?

Nash solution to the co-operative game

The players first find the Nash bargaining solution, which is denoted by N(S), simply by maximising Nash’s product (u_H-d_H)(u_W-d_W) in S:

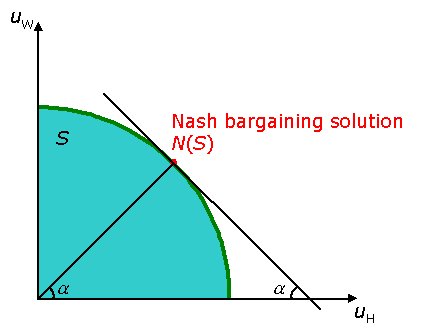
Geometrically it is found, for instance, by drawing a triangle such that its one side tangents the set S and one vertex is at the threat point (origin).

… the axioms behind the solution …

Nash’s solution N(S) is implied by the following axioms:

1. N(S) is Pareto optimal and jointly preferred to the disagreement point.

2. N(S) is independent of the units of the decision-makers: the solution does not vary if the utility of a decision-maker is multiplied by a positive constant.

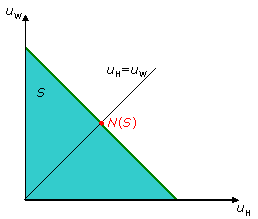
3. Symmetry: the utilities of the decision-makers at the solution are equal if the set S is symmetric. By definition, S is symmetric if the set S is not affected even if the roles of the players are changed, see figure below as an example for symmetrical set.

4. Independence of the irrelevant alternatives: if there is a negotiation set S and S is narrowed to produce a new smaller negotiation set S’ such that the N(S) is in S’, then N(S’) = N(S), see figure below for illustration.

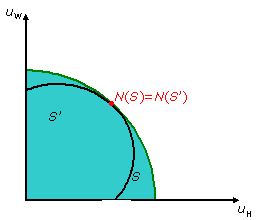
… so what? …

Should Harold and William accept N(S)? Is it fair solution? If they consider the axioms fair so perhaps they should make an agreement.

… some criticism …

Nash’s fourth axiom, independence of irrelevant alternatives, has been the source of considerable contention. Imagine that the game is modified such that its representation in the utility set is as in figure below.

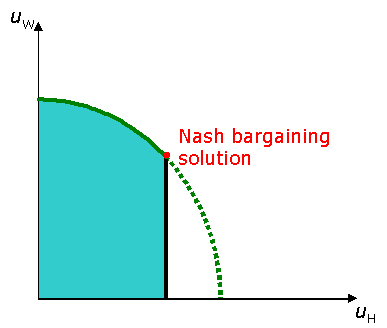
Due to the axiom of irrelevant alternatives the original and the modified game have the Nash bargaining solution in common. The dilemma is, that Harold obtains maximal payoff and William achieves only about 80% of the maximal payoff in the modified case.

Kalai-Smodrodinsky solution

Kalai and Smorodinsky (1975) modified the axioms presented by Nash. They replaced his arguing fourth axiom by monotonicity axiom:

4’. If the negotiation set S is enlargened such that the maximum utilities of the players remain unchanged, then neither of the players must not suffer from it.

… its graphical representation …

This solution concept can be described graphically, as well. Define an ideal point a(S) gives the maximum payoff for Harold and William separately, see the figure below.

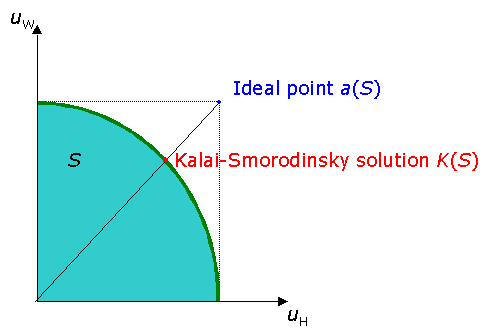
Now, connect the origin and that ideal point by a line segment. The Kalai-Smorodinsky solution K(S) is maximal point in S on that line segment.